Expected Value of a Lawsuit
Introduction
At its core, a lawsuit is a kind of bet. Estimating a lawsuit’s value, therefore, is just figuring out how good or bad of a bet it is. A lawsuit’s value, in turn, is a key factor in making important litigation decisions, such as whether to file a lawsuit at all or for how much to settle that lawsuit. A typical approach is to think of a lawsuit’s value as a function of
- the payoff of every possible outcome of the lawsuit
- for each possible outcome, the probability that it will occur; and
- for each possible outcome, the cost you’d need to incur to make that outcome happen
With this in mind, let’s estimate a lawsuit’s expected value, that is, the average probability-weighted net payoff for each potential lawsuit outcome. Then, we can use that value to help us make some litigation decisions.
That’s all actually simpler than it sounds! What follows is a gentle introduction to the extensive literature for lawyers on litigation risk analysis (e.g., Biedermann and Koehler 2022; Keet, Heavin, and Lande 2020, chap. 5; Aaron 2019; Celona 2016; Victor 2015).
If this seems a little weird, here are three reasons to motivate you. First, sophisticated lawyers today either typically think of litigation in this way, or must communicate in this way to sophisticated clients and other non-lawyers. Demand for this skill will increase as data analytics (e.g., machine-learning) spreads throughout the legal profession, precisely because as compared to other legal tasks, this skill has proved (for now) difficult to automate (Kapoor, Henderson, and Narayanan 2024).
Second, legal strategy often requires asking how much a lawsuit’s expected value changes, depending on the legal arguments a lawyer might make. Thus, a lawyer can’t be a good strategist about what to argue without first becoming a good prediction engine about litigation outcomes.
Third, past research finds that lawyers and law students are no less vulnerable to cognitive biases that hamper accurate prediction generally (e.g., Goodman-Delahunty et al. 2010; Melnikoff and Strohminger 2020; Jeklic 2023) and, like all humans, exhibit bias in how they process information (e.g. Oeberst and Imhoff 2023). Accordingly, think of litigation risk analysis as a countermeasure against such biases, particularly if paired with the countermeasure of actively generating arguments challenging your beliefs about what’s likely to occur.
A Simple Bet
Let’s start by recalling all those days before law school that you spent . . . gambling. Suppose I made you a bet: Pay me $12.50, and I’ll flip this coin. If it comes up “heads”, you win $40.00. But if it comes up “tails”, you lose $30.00. Is it worth paying me $12.50 to take this bet? How can you know how much this bet is worth, if you don’t know yet which way the coin will flip?
You’d start first by assigning probabilities to how likely the coin will come up “heads” or “tails”, given some background knowledge or assumptions. In doing that, you’re just assigning a number (between 0 and 1) that expresses how plausible it is that the proposition of interest (coin comes up “heads”) is true, given your background information. Here, that’s just what you’ve read, been told, or experienced about coins and how they flip. That’s fine, so long as you can identify and justify your background assumptions.
NoteWhat’s a Probability?
A probability denotes the degree of plausible belief in any proposition \(X\), given what you already know or assume (\(\mathcal{I}\)). For example, if X = Eight planets orbit our sun, then \(Pr(X \mid \mathcal{I})\) is shorthand for the how much you can plausibly believe that Eight planets orbit our sun is true, given what you know or take as true about planets, our solar system, and other background assumptions.
Any probability is expressed as a number between 0 and 1 (e.g. \(P(X \mid \mathcal{I})\) = 0.25), with “0” denoting certainly false and “1” denoting certainly true. We can equivalently express that probability as a percentage, e.g., 25% ; a fraction (=\(\frac{25}{100} = \frac{1}{4}\)); and a frequency (“25 out of 100”).
We can also convert a probability into odds and vice-versa. For any probability \(p\) of a proposition \(X\), the corresponding odds of \(X\) is \(\frac{p}{1 - p}\). For example, a probability of 0.25 equals an odds of \(\frac{0.25}{1 - 0.25} = \frac{1}{3}\). Conversely for any odds of \(X\), the corresponding probability \(p = \frac{\text{odds}}{1 + \text{odds}}\). So, an odds of \(\frac{1}{3}\) equals a probability of \(\frac{\frac{1}{3}}{\frac{4}{3}} = 0.25\).
What background information led you to assign these probabilities? Maybe you put this coin in the palm of your hand and, based on its shape and weight, believe that someone modified it to give “heads” an edge. Or maybe I let you flip this coin ten times beforehand, and you got “heads” about 6 out of 10 times. Or you assume that “heads” is bit more likely than “tails”, based on observing my behavior and surmising that, in offering bets, I’m a bit of shady con-artist character.
Suppose your best guess is that the outcome “heads” is 55% likely to occur. That means that “tails” is 45% likely to occur, because the probabilities of all possible outcomes – “heads” and “tails” – should sum to 1. In assigning a 55% probability for “heads”, you’ve distilled all of your background information into that number.
Now, account for cost. Remember, you’ve got to pay me $12.50 to take the bet, regardless of whether you win or lose. If you win, you’d only really take home $27.50. If you lose, you’d really lose $42.50.
Then, you’d adjust for how likely each net outcome is by multiplying how likely it is with its net payoff.
- Heads = 55% \(\times\) $27.50 = $15.13.
- Tails = 45% \(\times\) $-42.50 = $-19.12.
Add those numbers up: $15.13 + $-19.12 = $-4.00, which is the expected value of this bet.
This means that if you repeatedly made this bet, and each bet didn’t depend on the outcome of any previous bet, as the number of bets increase, your average net payoff would get closer and closer to $-4.00.
Would you take this bet? No! Walk away! We’re assuming that you get no thrill or anxiety from the act of gambling itself.
In each of the following problems, the bet is the lawsuit, and we follow the same approach to estimating that lawsuit’s expected value.
A Simple Problem
Suppose D offers you $40,000 to settle your tort claim. (I’m using tort claims in these examples, but the same approach applies regardless the claim’s source of law.) Your cost of accepting settlement = $0. At the time, you believe that if you go to trial instead, you have a 55% chance of winning. If you win, you believe you’ll get a $100,000 damages award. If you lose, you get $0. Going to trial will cost you $20,000 if you win, and $20,000 if you lose.
Question: Should you accept the settlement offer?
Answer: Yes, because the net expected value of your claim is $35,000, which is less than the settlement offer.
To see how this works, think about the lawsuit as having only two possible outcomes: (A) You win by proving liability, or (B) you don’t, and you lose. Sure, a lot of things can happen as a result of a lawsuit, but we simplify, because these two outcomes are the only ones that we care about.
In turn, each outcome has a payoff:
- outcome (A): $100,000
- outcome (B): $0.
To simplify, we’re assuming that you only care about the damage award you could get if you win. In fact, lawsuits have many types of payoffs, not just money damages. These include injunctive relief, a public declaration of the defendant’s liability, establishing a precedent that others might use, the change in behavior in others (non-defendants) that might occur as a result of your lawsuit victory, fame or social honor, or just a feeling of satisfaction. Whatever the non-monetary payoffs, you can assign them a monetary value, after which you’d take the sum of any damages award and the non-monetary payoffs to get the lawsuit’s total payoff.
In any case, you believe that outcome A has a 55% of chance of occurring, given background information \(\mathcal{I}\) based on prior knowledge or experience. This can include not only what the law on paper says but also your prior beliefs about the judge, the available evidence, and other court characteristics. Then, outcome B (the only other possible outcome) has a 45% of chance of occurring, given the same background information. Put another way,
- \(P(A| trial, \mathcal{I})\) = 0.55
- \(P(B| trial, \mathcal{I})\) = 0.45
Read “|” in the above as “given”, as in “the probability of outcome A, given that a trial occurs and the background information you already have”.
Let’s depict the structure of this problem as a decision tree.
Here’s how to read Figure 1. The rectangle indicates a decision point (here, settle or go to trial). Follow the arrows from there to each triangle, which denotes each possible outcome (“settle”, “A”, “B”) and its accompanying payoff. The circle denotes a chance event on a path between decision and outcome, with the probability of each outcome (here, 0.55 and 0.45) appearing on each path (the arrow line) between event and outcome.
In all, this lawsuit has three possible paths from decision point to outcome:
- decide —> settle
- decide –> trial –> A
- decide –> trial –> B
We can now get the expected value of the lawsuit in three steps.
First, adjust each outcome for cost. Here, if you win, you’ll have incurred $20,000 to go to trial. If you lose, you’ll still have incurred $20,000 to go to trial. (To make it simple, we’re assuming that you, not anyone else, bears the total cost of going to trial.) So, the net payoffs for each outcome (payoff minus cost) are:
- For outcome (A), $80,000.
- For outcome (B), $-20,000.
Second, for each trial outcome, calculate its probability-weighted net payoff. How? Just multiply each outcome’s probability with its net payoff, as follows:
- For outcome (A), that’s 0.55 \(\times\) $80,000 = $44,000.
- For outcome (B), that’s 0.45 \(\times\) $-20,000 = $-9,000.
Here is what we’ve done thus far:
| Outcomes | Probability | Payoff | Cost | Net Payoff | Adj Payoff |
|---|---|---|---|---|---|
| A | 0.55 | $100,000 | $20,000 | $80,000 | $44,000 |
| B | 0.45 | $0 | $20,000 | $-20,000 | $-9,000 |
Third, sum the adjusted payoffs of all the outcomes (the last column in Table 1), i.e. $44,000 + $-9,000 = $35,000.
Now, update the decision tree by adding this value to the tree node associated with going to trial.
Decision Tree with Trial Node Completed
Now, compare the lawsuit’s net expected value ($35,000) and the settlement offer ($40,000), and see which is larger. If the settlement offer is larger, then you should take the settlement offer. If not, you should take the other path and go to trial.
More Than Two Outcomes
D offers you $42,500 to settle your tort claim. Based on information about trial outcomes of claims like yours, you believe that if you go to trial, you have (A) a 50% chance of winning $100,000, (B) a 30% chance of winning $20,000, and (C) a 20% of losing (winning $0). Going to trial will cost you $10,000. Assume the cost of settlement = $0.
Question: Should you accept the settlement offer?
Figure 2 depicts our initial decision tree.
This problem is more complicated than Problem 1 only because there are three potential outcomes, not just two. Otherwise, you’d solve it in the same way.
Here are the intermediate calculations:
| Outcomes | Probability | Payoff | Cost | Net Payoff | Adj Payoff |
|---|---|---|---|---|---|
| A | 0.5 | $100,000 | $10,000 | $90,000 | $45,000 |
| B | 0.3 | $20,000 | $10,000 | $10,000 | $3,000 |
| C | 0.2 | $0 | $10,000 | $-10,000 | $-2,000 |
Answer: No. The net expected value of your lawsuit is $46,000, which is greater than the settlement offer.
Here is a final version of the decision tree.
When Litigation Costs Vary
D offers you $42,500 to settle your tort claim. Based on information about trial outcomes of claims like yours (your background information), you believe that if you go to trial, you have (A) a 50% chance of winning $100,000, (B) a 30% chance of winning $20,000, and (C) a 20% of losing (winning $0). You believe that going to trial will cost you $10,000, and that outcome (A) will require an additional cost of $12,000 to hire an expert witness. Assume the cost of settlement = $0.
Should you accept the settlement offer?
Answer: Yes. The net expected value of your lawsuit is $40,000, which is less than the settlement offer.
| Outcomes | Probability | Payoff | Cost | Net Payoff | Adj Payoff |
|---|---|---|---|---|---|
| A | 0.5 | $100,000 | $22,000 | $78,000 | $39,000 |
| B | 0.3 | $20,000 | $10,000 | $10,000 | $3,000 |
| C | 0.2 | $0 | $10,000 | $-10,000 | $-2,000 |
This problem is like the previous ones except the the cost associated with each outcome varies.
How would you solve this problem differently if the lawyer, not the client, agreed to bear litigation costs under a contingency fee agreement?
Sequences of Chance Events
D offers you $42,500 to settle your tort claim. Based on your background information about outcomes of claims like yours, you believe that if you go to trial, you have (A) a 80% chance of a judgment declaring the defendant is liable, and (B) a 20% chance of a judgment finding no liability. If you do get a judgment of liability, you believe that the jury is (C) 55% likely to award $100,000, (D) 35% likely to award $50,000; and (E) 10% likely to award $500,000. Assume that going to trial will cost you $10,000, regardless of which outcome occurs, and that the cost of settlement = $0.
Should you accept the settlement offer?
For this problem, the lawsuit’s expected value depends on more than one chance event on a path from decision to outcome, because the net payoff of (A) depends on how likely outcomes (C), (D), and (E) are to occur.
Initial Decision Tree
No worries! Just break it into two separate problems.
First, add up the probability-adjusted payoffs of (C), (D), and (E), which is $122,500.
| Outcomes | Probability | Payoff | Cost | Net Payoff | Adj Payoff |
|---|---|---|---|---|---|
| C | 0.55 | $100,000 | $0 | $100,000 | $55,000 |
| D | 0.35 | $50,000 | $0 | $50,000 | $17,500 |
| E | 0.10 | $500,000 | $0 | $500,000 | $50,000 |
Second, using $122,500 as the payoff for outcome (A), take the sum of the probability-weighted payoffs of (A) and (B), making sure this time to subtract the cost of going to trial.
| Outcomes | Probability | Payoff | Cost | Net Payoff | Adj Payoff |
|---|---|---|---|---|---|
| A | 0.8 | $122,500 | $10,000 | $112,500 | $90,000 |
| B | 0.2 | $0 | $10,000 | $-10,000 | $-2,000 |
Answer: No. The net expected value of your lawsuit is $88,000, which is greater than the settlement offer.
Here is the decision tree, with probabilities, payoffs, and the associated calculations already completed.
Damages Cap
D offers you $42,500 to settle your tort claim. Based on information about trial outcomes of claims like yours, you believe that if you go to trial, you have (A) a 80% chance of get a judgment declaring the defendant is liable, and (B) a 20% chance of a judgment finding no liability. If you do get a judgment of liability, you believe that the jury is (C) 55% likely to award $100,000, (D) 35% likely to award $50,000; and (E) 10% likely to award $500,0000. Assume that going to trial will cost you $10,000, regardless of which outcome occurs. Assume the cost of settlement = $0. Your jurisdiction also has a statute that caps total damages for tort claims at $300,000 per lawsuit.
Should you accept the settlement offer?
This is the same problem as the previous one, except we need to account for the $300,000 damages cap. How? Just treat it as another chance event.
To illustrate, suppose I believe that, if outcome (E) occurs, there is a 90% chance that, because of the damages cap, the defendant will file and the trial judge will grant, a post-verdict motion to reduce the award to $300,000. This implies a 10% chance that the trial judge will deny that motion (for whatever reason). (For simplicity, I assume zero costs incurred for arguing the post-verdict motion, and that the defendant will always file the motion.)
To account for this belief, we modify the structure of the decision tree by creating two new branches (E1 and E2) as follows:
Now, calculate the sum of the probability-weighted payoffs of outcomes (E1) and (E2), i.e., the sum of the amounts in the last column in Table 5.1.
| Outcomes | Probability | Payoff | Cost | Net Payoff | Adj Payoff |
|---|---|---|---|---|---|
| E1 | 0.9 | $300,000 | $0 | $300,000 | $270,000 |
| E2 | 0.1 | $500,000 | $0 | $500,000 | $50,000 |
Then, use that amount ($320,000) as the payoff for outcome (E), and calculate the sum of the probability-weighted payoffs of outcomes (C), (D), and (E).
| Outcomes | Probability | Payoff | Cost | Net Payoff | Adj Payoff |
|---|---|---|---|---|---|
| C | 0.55 | $100,000 | $0 | $100,000 | $55,000 |
| D | 0.35 | $50,000 | $0 | $50,000 | $17,500 |
| E | 0.10 | $320,000 | $0 | $320,000 | $32,000 |
Finally, use that amount ($104,500) as the payoff for outcome (A), take the sum of the probability-weighted payoffs of (A) and (B), making sure this time to subtract the cost of going to trial.
| Outcomes | Probability | Payoff | Cost | Net Payoff | Adj Payoff |
|---|---|---|---|---|---|
| A | 0.8 | $104,500 | $10,000 | $94,500 | $75,600 |
| B | 0.2 | $0 | $10,000 | $-10,000 | $-2,000 |
Answer: The net expected value of your lawsuit is $73,600, which is greater than the settlement offer.
A Complex Problem
Only for fun, consider the following more complex problem:
Your client has been sued by a long-time smoker with stomach cancer. He alleges that the cancer was caused by exposure to a chemical used in your operations for decades. Most scientific literature finds no association between the chemical and stomach cancer. Age 46, he now has only a few years to live, and will leave behind a wife and two teenage children. You have already filed a motion to dismiss, and are now awaiting a decision on that motion. Assume zero litigation costs and fees.
You believe the following:
There is an 80% chance the trial judge will deny the motion to dismiss on the issue of general causation (i.e., that the chemical does not cause stomach cancer).
There is a 10% chance that the jurors, after hearing the state of operations at your client’s plant, will ignore your defenses, declare your client “liable”, and jump straight to the question of damages.
If the jury does consider your two defenses, you have a 1-in-3 chance of convincing them that the plaintiff was not exposed to the chemical; even if they think he was, you still have a 1-in-4 chance of convincing them his exposure did not cause his stomach cancer.
If the jury holds your client liable after considering the defenses, there is a 25% chance they will award damages of around $8 million; a 50% chance of around $4 million; and a 25% chance of around $2 million.
If the jury does not consider your defenses, your estimate of high, medium, and low damages all go up by 25%.
If you put a settlement offer of $3.75 million on the table, should the plaintiff’s lawyer accept that offer?
Answer: Yes, provided that the plaintiff’s lawyer agrees with your estimate of the expected value of the plaintiff’s lawsuit.
Figure 4 is the decision tree, with probabilities, payoffs, and the associated calculations already completed.
Can you figure out how to arrive at this result based solely on the items of information provided above?
The Lurking Weasel
Thus far, I’ve provided you the probabilities for each possible outcome of interest. In the real world, you’ll have to do that yourself. And that’s hard to do well. As a result, you might feel some dread: ‘How am I supposed to know what those probabilities are? Who the heck knows? I sure don’t!’
And, what’s worse, too many lawyers resort to stock words and phrases, not numerical values, to describe their beliefs about the odds of litigation success: “very likely”, “a distinct possibility”, “a slam dunk”, “pretty good chance” and so on. If pressed, they might push back, decrying a numerical probability value as bogus precision - ‘Where’d you get that number? You’re just making it up, right?’ (Too many law professors would do the same.)
This strategy – using words instead of numbers to denote probability – isn’t unique to lawyers. In the 1960s, C.I.A. analyst Sherman Kent (1964) lamented that when faced with a “difficult but not impossible” task of predicting what would happen in Eastern Europe, the Soviet Union and elsewhere, his fellow intelligence analysts would avoid actual numerical probabilities and instead use vague words and phrases – what Kent called “the lurking weasel”:
How rich the spoken language in its vocabulary of issue ducking “I have a sneaker that … ,” “I’d drop dead of surprise if …” - expressions with sound but upon reflection almost without meaning. How much conviction, for example, do you have to have before you become possessed of a sneaker; how much of the unexpected does it take to cause your heart to fail? . . . . What we consciously or subconsciously seek is an expression which conveys a definite meaning but at the same time either absolves us completely of the responsibility or makes the estimate at enough removes from ourselves as not to implicate us.
Moreover, even when analysts used the same word or phrase, they sometimes had different numerical probabilities in mind. Imagine two people who told you that you had a “serious probability” of losing a lawsuit. Press further, and you might find one of them meant to indicate a 40% probability, while the other meant a 75% probability. In short, words and phrases can denote a wide range of numerical probabilities, as nicely illustrated by the results of one survey (Mauboussin and Mauboussin 2018).
As a partial solution, Kent proposed that intelligence analysts limit their words denoting probability to a small set of fixed phrases, each corresponding to a range of numerical probabilities. Today, the U.S. intelligence community follows that approach (Office of the Director of National Intelligence 2015, 3). Intelligence analysts, when making predictions, must use specific words and phrases for different probability ranges:
| words | probability |
|---|---|
| ‘almost no chance’ or ‘remote’ | 1%-5% |
| ‘very unlikely’ or ‘highly improbable’ | 5%-20% |
| ‘unlikely’ or ‘improbable’ | 20%-45% |
| ‘roughly even chance’ or ‘roughly even odds’ | 45%-55% |
| ‘likely’ or ‘probable (probably)’ | 55%-80% |
| ‘very likely’ or ‘highly probable’ | 80%-95% |
| ‘almost certain(ly)’ or ‘nearly certain’ | 95%-99% |
But, as the research literature indicates, there are many more problems with this kind of curated-words approach as compared to just using numerical probabilities alone (Dhami and Mandel 2020, 2022).
Meanwhile, however flawed that approach, lawyers don’t even have anything like this kind of curated-words guideline, even though decisions based on their legal predictions can affect their clients’ lives, liberty, and property. The lurking weasel abides.
What to do? Thwarting the weasel just takes a lot of practice. So, throughout this class, we’ll chat about assigning numerical probabilities to hypothetical legal events, such as the outcomes of legal motions or appeals, based on what we know about current law and past judicial opinions, what legal arguments we could make, and what we believe we can prove. Maybe it’ll be weird at first, but soon you’ll get the hang of it (and get better at spotting the lurking weasel too).
TipHow Sure Are You?
Later, when you feel ready, you can go further by communicating to clients and colleagues not only what you believe is the probability of an event (each circle in a litigation decision tree) but also how sure or certain you are about it.
Imagine that you’ve just explained your litigation-decision analysis (like the problems above) to a client, and the ensuing recommendation: Reject the settlement offer and go to trial. Suppose further that you’ve estimated that, if you go to trial, you have an eighty percent change of winning (0.80 or 80%). You explain all the reasons you think that 80% is the best estimate of that probability, based on the information you have. And then, someone asks: “How sure are you that it’s 80%, not something lower or higher?”
Are you tempted to respond by saying something like “Mostly sure”, “high/medium confidence” or “It’s a pretty fluid scenario” ?
Here is a better way. For each event, ask yourself three questions (in the following order) about its probability (expressed, say, as a number between 0 and 1), given what you currently know or believe:
- What is the lowest plausible value that probability could be (\(= a\))?
- What is the highest plausible value that probability could be (\(= b\))?
- What is the most-likely value of that probability (\(= m\))?
By “plausible” value, I mean that if I told you that the true value fell below it, you should react by thinking I’d erred in calculating or reporting it. If you don’t react that way, revise \(a\) (lower) and \(b\) (higher) until you do.
Make sure that \(a \leq m \leq b\).
Now, take the optimistic value (\(a\)) and pessimistic value (\(b\)) and calculate the difference (\(= b - a\)). This difference roughly measures how sure or certain you are about your probability estimate. The smaller or larger that difference, the more or less sure or certain you feel about it. If that difference is zero, then you feel completely certain (\(a = m = b\)).
Next, insert as many different values between \(a\) and \(b\) into your litigation-risk analysis, and see whether or not the recommended final decision changes.
To illustrate, consider the first problem above (Section 3, “A Simple Problem”). In that problem, we assumed a 55% probability of winning, if we went to trial; calculated a net expected value of $35,000; and concluded that we should take the settlement offer. Suppose you believed that the lowest and highest plausible probabilities of winning a trial are 30% and 75%.
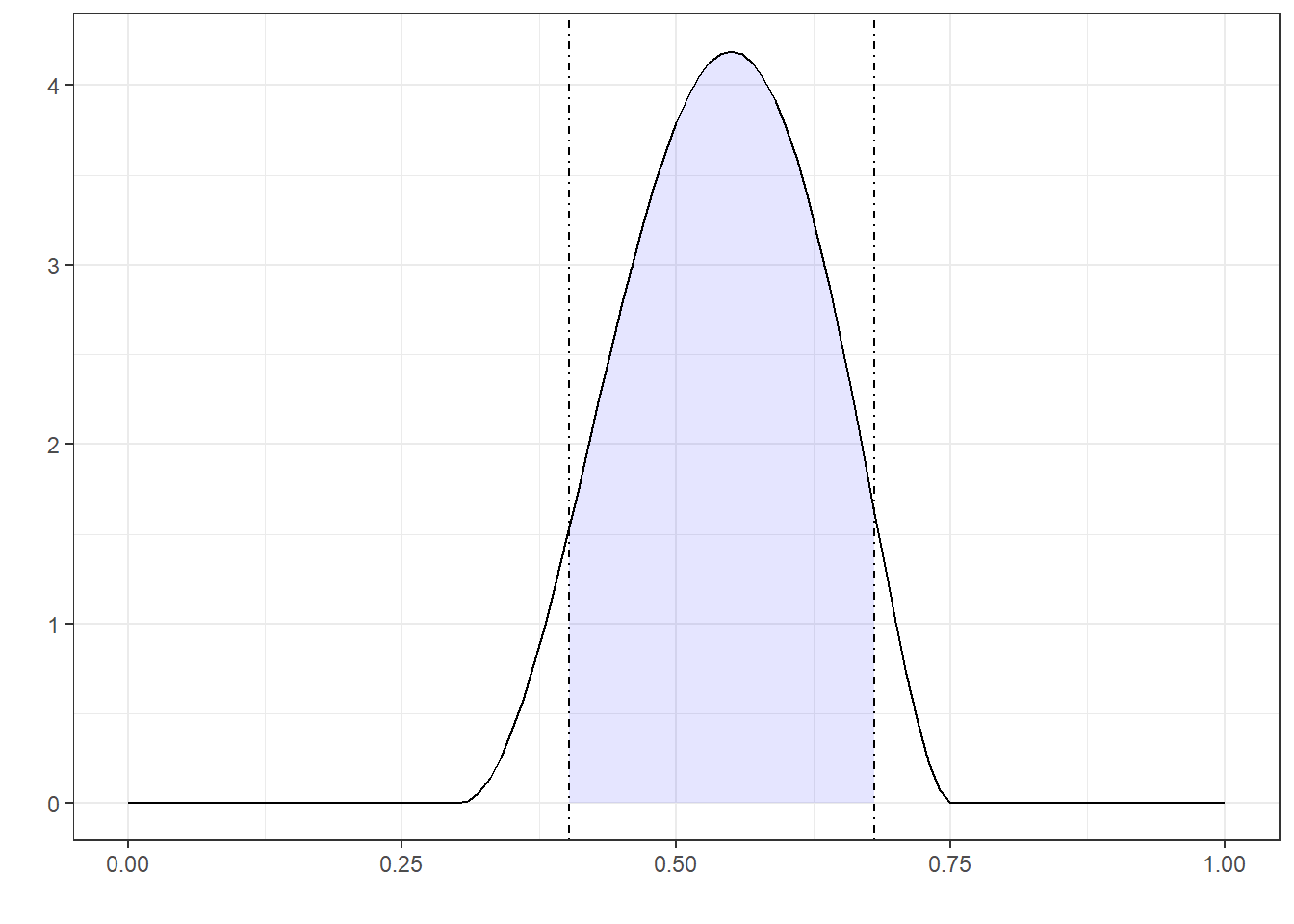
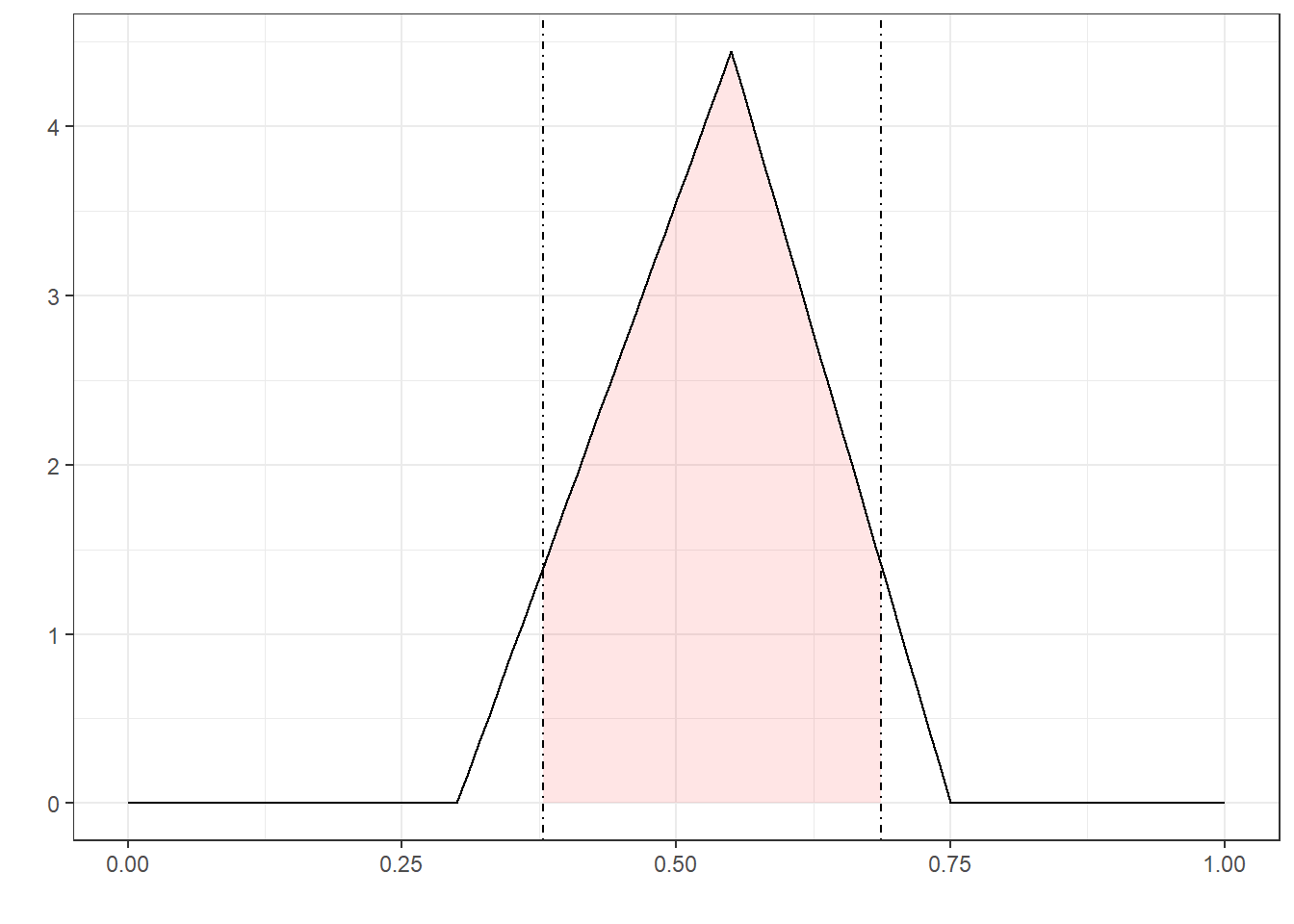
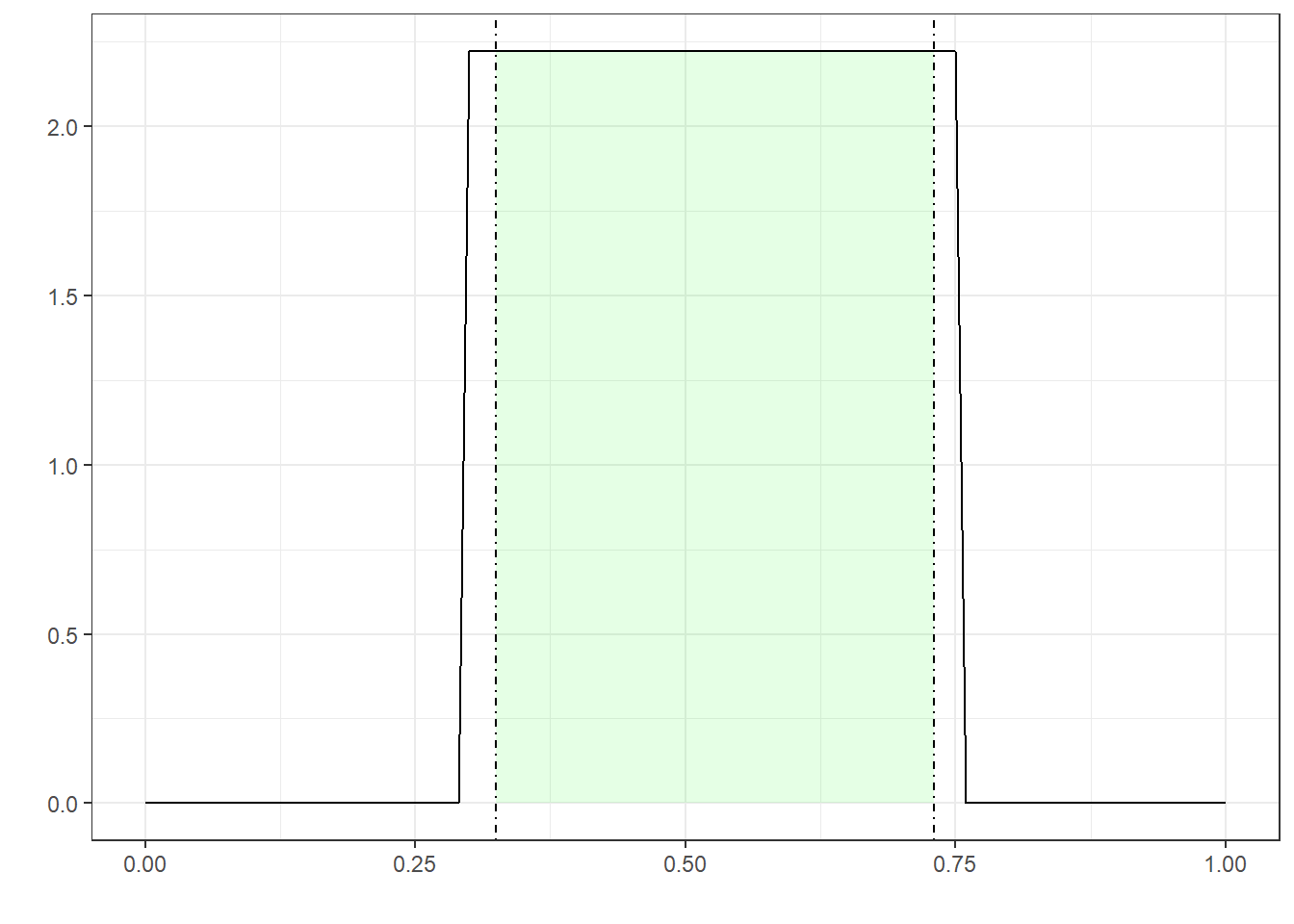
For those of you who like to think in pictures, Figure 5 (a), Figure 5 (b), and Figure 5 (c) depict three possible ways of extrapolating a distribution of likely probability values, given these values for \(a\), \(m\), and \(b\). (For details, see Vose (2008), pg. 403-407.) Eighty-nine percent of these values fall within the dot-dashed lines. Which such values, if true, would lead you to recommend going to trial as opposed to settling?
Finally, justify your predictions – including your answers to \(a\), \(b\), and \(m\) – and the ensuing decision analysis by explaining to your client or colleagues how you reached it; what new information would lead you revise your prediction(s) enough to actually change what you recommend; and how sensitive your recommendation is, given how sure you are about the probabilities you’ve assigned.
Conclusion
Remember, you can estimate a lawsuit’s value only as well as you identify the salient structure of outcomes, payoffs, and probabilities. Once you do, decision-tree software can help. For an open source option, see Kamiński et al. (n.d.). Overall, think of this approach as helping you avoid the garbage-out problem, i.e., errors and biases in how you use background information to evaluate how much a lawsuit is worth. This approach will also help you explain to clients why you recommend a particular course of action.
Colophon
Figures produced with Silver Decisions (Kamiński et al. n.d.) and DiagrammeR (Iannone and Roy 2024).
References
Aaron, Marjorie Corman. 2019. Risk & Rigor: A Lawyer’s Guide to Decision Trees for Assessing Cases and Advising Clients. DRI Press. https://open.mitchellhamline.edu/dri_press/9.
Biedermann, Alex, and Jonathan J. Koehler. 2022. “Influence Diagrams for Complex Litigation.” Jurimetrics Journal 62 (1): 131–71.
Celona, John. 2016. Winning at Litigation Through Decision Analysis: Creating and Executing Winning Strategies in Any Litigation or Dispute. Springer. https://doi.org/10.1007/978-3-319-30040-5.
Dhami, Mandeep K., and David R. Mandel. 2020. “Words or Numbers? Communicating Probability in Intelligence Analysis.” American Psychologist 76: 549–60. https://doi.org/10.1037/amp0000637.
———. 2022. “Communicating Uncertainty Using Words and Numbers.” Trends in Cognitive Sciences 26 (6): 514–26. https://doi.org/10.1016/j.tics.2022.03.002.
Goodman-Delahunty, Jane, Pär Anders Granhag, Maria Hartwig, and Elizabeth F. Loftus. 2010. “Insightful or Wishful: Lawyers’ Ability to Predict Case Outcomes.” Psychology, Public Policy, and Law 16 (2): 133–57. https://doi.org/10.1037/a0019060.
Iannone, Richard, and Olivier Roy. 2024. DiagrammeR: Graph/Network Visualization. https://doi.org/10.32614/CRAN.package.DiagrammeR.
Jeklic, Mihael A. 2023. “Can You Trust Your Lawyer’s Call? Legal Advisers Exhibit Myside Bias Resistant to Debiasing Interventions.” Journal of Empirical Legal Studies 20 (2): 409–33. https://doi.org/10.1111/jels.12350.
Kamiński, Bogumił, Przemysław Szufel, Michał Wasiluk, Michał Jakubczyk, Marcin Czupryna, and Anna Wiertlewska. n.d. “Silver Decisions.” Accessed January 18, 2021. http://www.silverdecisions.pl.
Kapoor, Sayash, Peter Henderson, and Arvind Narayanan. 2024. “Promises and Pitfalls of Artificial Intelligence for Legal Applications.” Journal of Cross-Disciplinary Research in Computational Law 2 (2). https://journalcrcl.org/crcl/article/view/62.
Keet, Michaela, Heather Heavin, and John Lande. 2020. Litigation Interest and Risk Assessment : Help Your Clients Make Good Litigation Decisions. Chicago: American Bar Association.
Kent, Sherman. 1964. “Words of Estimative Probability.” Studies in Intelligence 8 (4): 49–65. https://www.cia.gov/static/0aae8f84700a256abf63f7aad73b0a7d/Words-of-Estimative-Probability.pdf.
Mauboussin, Andrew, and Michael J. Mauboussin. 2018. “If You Say Something Is ‘Likely,’ How Likely Do People Think It Is.” Harvard Business Review 3 (July). https://hbr.org/2018/07/if-you-say-something-is-likely-how-likely-do-people-think-it-is.
Melnikoff, David E., and Nina Strohminger. 2020. “The Automatic Influence of Advocacy on Lawyers and Novices.” Nature Human Behaviour 4 (12): 1258–64. https://doi.org/10.1038/s41562-020-00943-3.
Oeberst, Aileen, and Roland Imhoff. 2023. “Toward Parsimony in Bias Research: A Proposed Common Framework of Belief-Consistent Information Processing for a Set of Biases.” Perspectives on Psychological Science 18 (6): 1464–87. https://doi.org/10.1177/17456916221148147.
Office of the Director of National Intelligence. 2015. “Intelligence Community Directive 203: Analytic Standards.” January 2, 2015. https://www.dni.gov/files/documents/ICD/ICD%20203%20Analytic%20Standards.pdf.
Victor, Marc B. 2015. “Decision Tree Analysis: A Means of Reducing Litigation Uncertainty and Facilitating Good Settlements.” Georgia State University Law Review 31 (4): 715–39. https://readingroom.law.gsu.edu/gsulr/vol31/iss4/3.
Vose, David. 2008. Risk Analysis: A Quantitative Guide. 3rd ed. John Wiley & Sons.